Implementing Softmax From Scratch: Avoiding the Numerical Stability Trap

In deep learning, classification models don’t just need to make predictions—they need to express confidence. This is where Softmax’s activation function comes in. Softmax takes the raw, infinite points generated by the neural network and transforms them into well-defined probability distributions, making it possible to interpret each output as the probability of a particular class.
This architecture makes Softmax the cornerstone of many classification tasks, from image recognition to language modeling. In this article, we will build an accurate understanding of how Softmax works and why the details of its use are more important than they first appear. Check it out FULL CODES here.
Using Naive Softmax
import torch
def softmax_naive(logits):
exp_logits = torch.exp(logits)
return exp_logits / exp_logits.sum(dim=1, keepdim=True)This exercise uses Softmax in its most straightforward form. It specifies each log and normalizes it by the sum of all values specified in all categories, generating a probability distribution for each input sample.
Although this implementation is mathematically correct and easy to learn, it is not statistically stable—large negative logs can cause overflow, and large negative logs can flow to zero. As a result, this version should be avoided in real training lines. Check it out FULL CODES here.
Sample Log and Target Labels
This example defines a small batch with three samples and three classes to represent both normal and failed conditions. The first and third samples contain meaningful logit values and behave as expected during the Softmax calculation. The second sample intentionally includes extreme values (1000 and -1000) to show numerical instability—this is where the arbitrary Softmax implementation breaks down.
The target tensor specifies the appropriate class index for each sample and will be used to calculate the phase loss and observe how the instability propagates during the backpropagation. Check it out FULL CODES here.
# Batch of 3 samples, 3 classes
logits = torch.tensor([
[2.0, 1.0, 0.1],
[1000.0, 1.0, -1000.0],
[3.0, 2.0, 1.0]
], requires_grad=True)
targets = torch.tensor([0, 2, 1])Forward Pass: Softmax Output and Failure Case
During the forward pass, a naive Softmax function is applied to the log to generate class probabilities. For normal logit values (first and third samples), the output is a valid probability distribution where the values are between 0 and 1 and sum to 1.
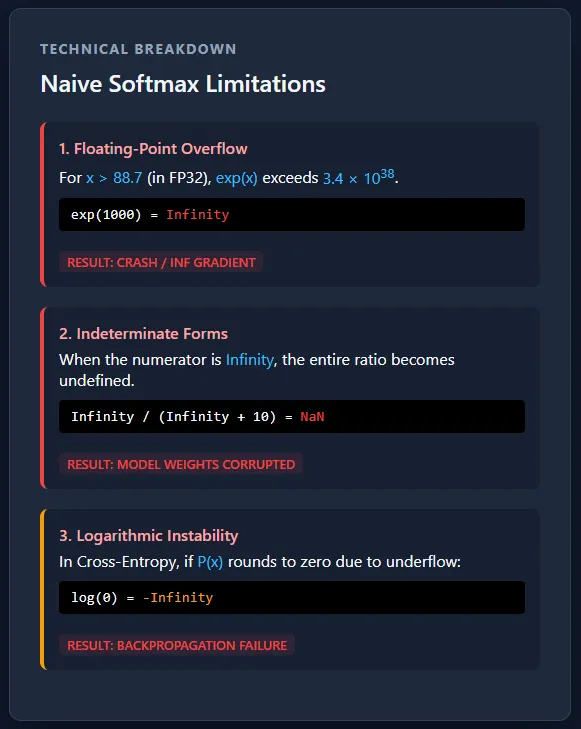
However, the second sample clearly reveals a numerical problem: to express 1000 overflows in infinitewhile -1000 goes under zero. This results in an invalid operation during normalization, which produces NaN values and zero probabilities. Once And N appears at this stage, contaminating all subsequent calculations, making the model unusable for training. Check it out FULL CODES here.
# Forward pass
probs = softmax_naive(logits)
print("Softmax probabilities:")
print(probs)Target Probability and Loss Classification
Here, we extract the predicted probabilities corresponding to the true class of each sample. While the first and third samples return valid probabilities, the target probability of the second sample is 0.0, which is caused by the small number flow in the Softmax calculation. When losses are calculated using -log(p)taking the logarithm of 0.0 results in +∞.
This makes the total loss permanent, which is a significant failure during training. If the loss becomes infinite, the gradient calculation becomes unstable, leading to And Ns during redistribution and effectively stopping learning. Check it out FULL CODES here.
# Extract target probabilities
target_probs = probs[torch.arange(len(targets)), targets]
print("nTarget probabilities:")
print(target_probs)
# Compute loss
loss = -torch.log(target_probs).mean()
print("nLoss:", loss)Backpropagation: Gradient Corruption
When backpropagation is performed, the effect of infinite loss is immediately apparent. The gradients of the first and third samples remained limited because their Softmax results were well behaved. However, the second sample produces NaN gradients for all classes due to the log(0) function on the loss.
These NaNs propagate back through the network, polluting the weight update and breaking the training efficiency. This is why numerical instability at the Softmax–loss boundary is so dangerous—once NaNs appear, recovery is almost impossible without restarting training. Check it out FULL CODES here.
loss.backward()
print("nGradients:")
print(logits.grad)Numerical Instability and Its Effects
Splitting Softmax and cross-entropy creates numerical robustness risks due to exponential overflow and underflow. Large logs can push the probabilities to infinity or zero, resulting in log(0) and leading to NaN gradients that quickly spoil training. At a production scale, this is not a rare case but a certainty—without a stable, integrated implementation, massive multi-GPU training will fail unexpectedly.
The problem with numbers comes from the fact that computers cannot represent infinitely large or infinitely small numbers. Floating point formats like FP32 have strict limits on how large or small a value can be stored. When Softmax integrates exp(x), the large positive values grow so fast that they exceed the maximum representable number and turn to infinity, while the large negative values decrease rapidly to zero. If the value becomes infinite or zero, subsequent operations such as division or logarithms fail and produce invalid results. Check it out FULL CODES here.
Using Stable Cross-Entropy Loss Using LogSumExp
This implementation calculates the cross-entropy loss directly from the raw logit without explicitly calculating the Softmax likelihood. To maintain numerical robustness, the logs are first shifted by subtracting the peak value for each sample, ensuring that the exponentials stay within a safe range.
The LogSumExp trick is then used to calculate the normalization term, after which the original (unmodified) target log is subtracted to obtain the correct loss. This method avoids overflow, overflow, and NaN gradients, and shows how cross-entropy is used in production-grade deep learning applications. Check it out FULL CODES here.
def stable_cross_entropy(logits, targets):
# Find max logit per sample
max_logits, _ = torch.max(logits, dim=1, keepdim=True)
# Shift logits for numerical stability
shifted_logits = logits - max_logits
# Compute LogSumExp
log_sum_exp = torch.log(torch.sum(torch.exp(shifted_logits), dim=1)) + max_logits.squeeze(1)
# Compute loss using ORIGINAL logits
loss = log_sum_exp - logits[torch.arange(len(targets)), targets]
return loss.mean()Stable Forward and Backward Pass
Running a stable cross-entropy implementation on the extreme logarithm produces finite losses with well-defined gradients. Even if one sample contains very large values (1000 and -1000), the LogSumExp structure keeps all average calculations in a safe numerical range. As a result, the backpropagation completes successfully without generating NaNs, and each stage receives a logical gradient signal.
This confirms that the previously observed instabilities were not caused by the data itself, but by the arbitrary separation of Softmax and cross-entropy—a problem fully solved by using a stable, numerically integrated loss formulation. Check it out FULL CODES here.
logits = torch.tensor([
[2.0, 1.0, 0.1],
[1000.0, 1.0, -1000.0],
[3.0, 2.0, 1.0]
], requires_grad=True)
targets = torch.tensor([0, 2, 1])
loss = stable_cross_entropy(logits, targets)
print("Stable loss:", loss)
loss.backward()
print("nGradients:")
print(logits.grad)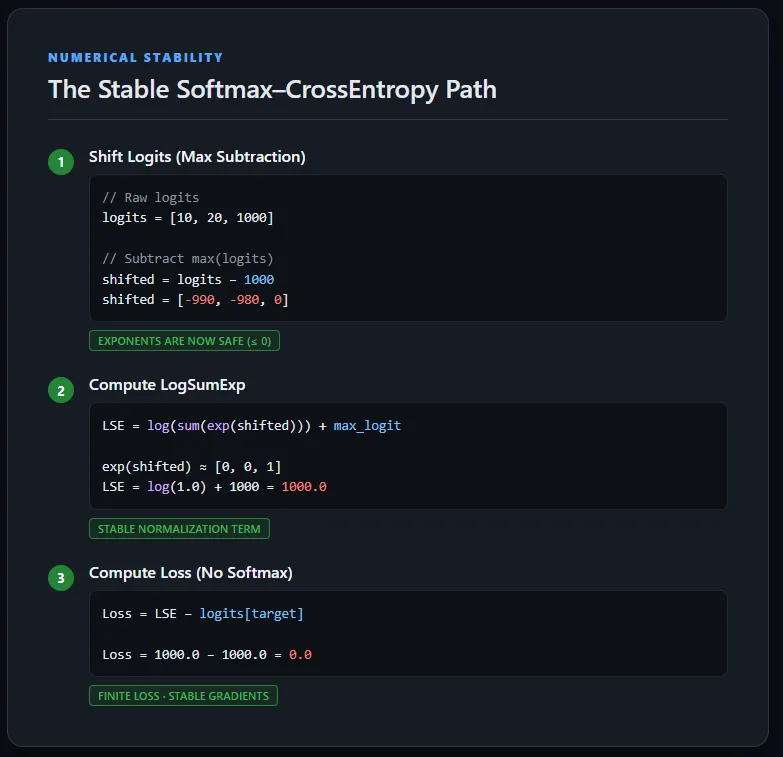

The conclusion
In fact, the gap between mathematical formulas and real-world code is where most training failures come from. Although Softmax and cross-entropy are mathematically well-defined, their arbitrary implementation ignores the limited accuracy limits of IEEE 754 hardware, making overflow and overflow inevitable.
Fixing the key is simple but critical: change logs before exposure and work on log background whenever possible. Most importantly, training rarely requires clear opportunities—sustainable entry opportunities are sufficient and very safe. When a loss suddenly turns into NaN in production, it’s usually a signal that Softmax is being manually computed in a place it shouldn’t be.
Check it out FULL CODES here. Also, feel free to follow us Twitter and don’t forget to join our 100k+ ML SubReddit and Subscribe to Our newspaper. Wait! are you on telegram? now you can join us on telegram too.
Check out our latest issue of ai2025.deva 2025-focused analytics platform that transforms model implementations, benchmarks, and ecosystem activity into structured datasets that you can sort, compare, and export

I am a Civil Engineering Graduate (2022) from Jamia Millia Islamia, New Delhi, and I am very interested in Data Science, especially Neural Networks and its application in various fields.



